LEV1ATHAN is an algorithm for generating level-1 networks from sets of rooted triplets, and forms the centrepoint of the article "A practical algorithm for reconstructing level-1 phylogenetic networks" by Huber, Van Iersel, Kelk and Suchecki. Specifically, it attempts to find a level-1 network consistent with as many of the input triplets as possible. To find the optimal such level-1 network is NP-hard. To circumvent this LEV1ATHAN uses, at its core, a polynomial-time heuristic based on ideas originally presented in "Algorithms for combining rooted triplets into a galled phylogenetic network" by Jansson, Nguyen and Sung. Huber et al have adapted and expanded this heuristic (see below for more details) and LEV1ATHAN is the Java implementation of the resulting algorithm.
The following instructions assume a UNIX environment. There are no fundamental reasons however why the algorithm will not work under another operating system environment as long as Java and a package capable of interpreting DOT files are available in that environment. A DOT interpreter is necessary (only) if the user wishes to convert the text output of the algorithm into a visual format. On our UNIX system the command dot does this for us. To be able to convert (collections) of newick files into triplets, or to convert sequence data into triplets, additional programs will be required, but this is optional and we shall return to this point later.
We have supplied all the relevant Java .class files as a .jar file, which in theory means that only a java interpreter is necessary to run the algorithm. However, it is recommended that the user recompiles the Java source on his/her own system, and for this access to the java compiler javac will be necessary. This can be done with the command,
javac -O Heuristic.java
If all goes well this should create (amongst others) the class file Heuristic.class. You can type
java Heuristic --help to see if the code has compiled correctly: if all is well a long help message
should appear that looks something like this:
LEV1ATHAN Version 1.0, 21 september 2009
----------------------------------------------
Usage: java Heuristic
----------------------------------------------
[options] can be:
--forcemaxsn : this forces the heuristic to -always- use the maximal SN-sets as the blocks of the partition. Only valid
when the input is dense. Default is false.
--noperfection : switches off the local perfection test. Default is
false.
--blocks [num]: this forces the heuristic to always partition into (at
most) [num] blocks. Default is 20.
--missing: this heuristic will display all triplets in the input that are
not consistent with the output network. Default is false.
--surplus: this heuristic will display all triplets in the output network
that are not consistent with the input. Default is false.
--sdweight [num]: when computing the symmetric difference, assume that
surplus triplets have weight [num] where [num] is a strictly positive
integer. Default is 1.
--sdradical: perform a radical SD-minimizing post-processing. Default is
false. Use in conjection with --sdweight. And with caution!
--wumax [num]: Wu's algorithm will not be used when there are more than
[num] leaves. Default is 10.
--simmax [num]: the exact simple level-1 algorithm will be used for up to
and including [num] leaves, the greedy algorithm after that. Default is
12.
--besttree: builds the optimum tree for the input, and quits. Is
exponentially slow! Default is false.
--bestsimple: builds the optimum simple level-1 network for the input, and
quits. Is exponentially slow! Default is false.
--bestgreedy: builds the greedy simple level-1 network for the input, and
quits. Default is false.
--nopostprocess: do not collapse redundant edges. Default is false
--nonetwork: do not output the network i.e. only output the statistics of
it. Default is false.
--dumpnettrips: prints every triplet (irrespective of whether it is in input) that is consistent with the final network to the file 'network.trips'.
Default is false.
--dumpconsistent: outputs to the file 'consistent.trips' the subset of input triplets (including weights) that are consistent with the final network.
Default is false.
--fortyeight: forces the program to produce (via derandomization) the best caterpillar network; this will be consistent with at least 48% of the input
triplets, but will be biologically not so meaningful. Switches all other
options off!
--say
--help: displays this message.
We begin by explaining the basic features of LEV1ATHAN, and by showing how the algorithm can be run without any complicated command-line options. We will do this with a walk-through example. (If you are interested in the algorithm at the heart of LEV1ATHAN then the control-flow of this algorithm is described here).
LEV1ATHAN takes as input a text file describing the rooted triplets. This text file has a very simple format. Each line has the form leaf leaf2 leaf3 [weight] and this denotes the triplet leaf1 leaf2 | leaf3, where [weight] is an optional field representing the weight of that triplet. (By default this weight value is assumed to be one. If given, it should be an integer greater than or equal to 1). Lines beginning with '//' are also allowed: these are considered comments and are ignored. We have included an example file of triplets here. This file contains 5787 unweighted triplets (i.e. all the triplets are assumed to have weight 1) on 33 leaves. Note that it is not allowed to have the same triplet occuring twice or more in the same input file: use the weight parameter instead.
We now run LEV1ATHAN on this dataset, without any command-line options, and analyse the output.
java Heuristic example.trips > example.out
(Alternatively, if you are using the JAR file, you can type java -jar Lev1athan.jar example.trips > example.out).You should get an output that looks something like this (depending on which version of the program you are using). We will analyse this in detail in a moment. At the most basic level it is only necessary to look at the second-to last line, // STAT: PERCENTAGE = 88.87. This line tells us that the Heuristic produced a network consistent with 88.87% of the (total weight of) the input triplets. Note that this line, like many of the lines in the output file, begins with //. This is because the output file has a second function: as a DOT file that can be fed into the graph drawing program that will produce a visual representation of the output network. DOT also uses // comments. So the output file can be viewed as a huge DOT file in which lots of extra information is hidden behind comments. We can turn the output file into an image like this,
dot -Tgif -o example.gif example.out
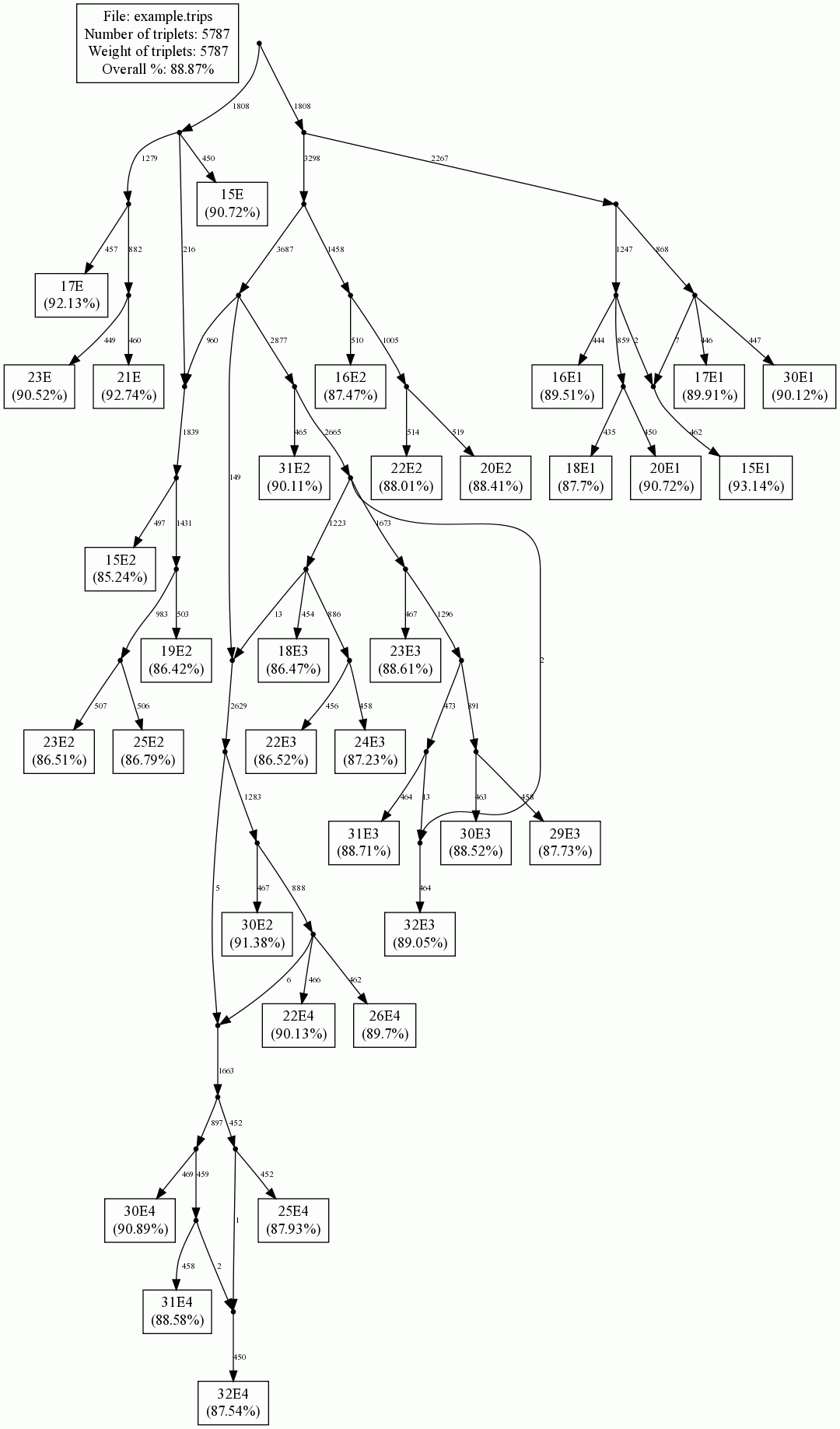
If all goes well, example.gif should be an image that looks a bit like this:

The numbers in the leaves, and on the edges, can be interpreted as follows. Within each leaf is a percentage, for example leaf 25E4 contains the percentage 87.93%. This means: this network is consistent with 87.93% of the (total weight of) the set of input triplets that contained leaf 25E4. Clearly, if the network is consistent with 100% of the input triplets, then the percentages in the leaves will also be 100%. The number on an edge, for example the 452 above leave 25E4, means: if this edge was deleted then the network would lose consistency with 452 units of triplet weight.
Notice also that some vertices have an outdegree higher than 2. LEV1ATHAN actually internally generates networks that have outdegree at most 2. It is also possible to see this network, as we shall discuss later. But the default LEV1ATHAN option is to mildly post-process this internally produced network. Mild post-processing means the repeated application of the following transformation: if there is an edge in the network such that neither endpoint is a reticulation vertex, and such that the contraction of this edge (i.e. identification of both endpoints) does not lead to any triplets being lost, then contract this edge. Parsimony is the motivation behind this, because contracting such an edge is tantamount to weaking our hypothesis of how the 'real' network should look like. Expressed in the language of symmetric difference (which we will elaborate on below): mild post-processing (potentially) lowers the symmetric difference, without damagaging any triplets.
That's pretty much the minimum amount of information you need to be able to use, and analyse the output, of LEV1ATHAN. What follows is a more detailed analysis.
A detailed look at the example output file
// LEV1ATHAN Version 1.0, 21 september 2009
// COMMENT: Pre-processing the input file to count the leaves
// COMMENT: Pre-processing showed that there are 33 leaves in the input.
// SUMMARY: Input had 33 leaves.
// COMMENT: Triplet set is already dense.
// SUMMARY: There are 5787 triplets in the input.
// SUMMARY: Total weight of input triplets is 5787.
Lines that begin with // COMMENT: are general messages given by the algorithm once it is executing.
Lines that begin with // SUMMARY:, are, as the name suggests, lines whereby important information is summarised to you.
// COMMENT: We achieved non-trivial local perfection.
// COMMENT: We achieved non-trivial local perfection.
// COMMENT: We achieved non-trivial local perfection.
// SUMMARY: (Before post-processing)
// SUMMARY: We got 5143 units of triplet weight, that's 88.87% of total weight.
// SUMMARY: In total 644 units of triplet weight were -not- consistent with the ouput network.
// SUMMARY: Output network contained 1544 triplets -not- in the original input.
// SUMMARY: The symmetric difference is thus 644 + (1 * 1544) = 2188
// SUMMARY: (After post-processing)
The particular cryptic-sounding COMMENTs shown here (about non-trivial local perfection) are what the algorithm prints when it notices, at some recursion level, that the maximum SN-sets induce a dense set of triplets that are consistent with a simple level-1 network. (In other words, that a JNS-move is possible, see article). The line // SUMMARY: (Before post-processing) heralds the end of the first, most important phase of the algorithm: by this stage the overall structure of the network is already known. The few lines after this explain the main properties of this network. Namely: (a) the percentage of the total input triplets weight that this network is consistent with; (b) the total amount of triplet weight that it is NOT consistent with; (c) the total weight of triplets that are consistent with the network, but are not in the input. An obvious question is: what is the weight of triplets that are not in the input? The default is 1, but this can be changed (see later). On the basis of these figures the (network-triplet) symmetric difference (SD) is computed: this is equal to the weight of input triplets that are not consistent with the ouput network PLUS the weight mentioned in (c). Please note, LEV1ATHAN was not primarily designed to optimise (i.e. minimize) SD but such statistics are included to give the user more insight into the quality of the solution.
The line // SUMMARY: (After post-processing) says that the post-processing phase is about to begin. As mentioned above, this is by default only mild post-processing. (Post-processing, even mild post-processing, can be computationally quite intensive, and this can be a reason to want to switch it off). In any case, after the post-processing phase is completed (or omitted) the next step is to produce the final network in DOT format. This is the region of the output file with the following form:
strict digraph G1 {
...
}
The closing lines of the example output file are as follows:
// SUMMARY: eNewick output:
((((15E2,(19E2,(23E2,25E2))))#H1,15E,(17E,(21E,23E))),((((15E1)#H2,30E1,17E1),(#H2,(18E1,20E1),16E1)),((16E2,(22E2,20E2)),(#H1,(((((30E4,((32E4)#H3,31E4)),(25E4,#H3)))#H4,(30E2,(#H4,22E4,26E4))))#H5,(31E2,((#H5,18E3,(22E3,24E3)),((((32E3)#H6,31E3),(29E3,30E3)),23E3),#H6))))));
// SUMMARY: In total 644 units of triplet weight were -not- consistent with the ouput network.
// SUMMARY: Output network contained 1544 triplets -not- in the original input.
// SUMMARY: Weight of missing triplets before contraction minus weight of missing triplets afterwards: 0
// SUMMARY: Number of surplus triplets before contraction minus number of surplus triplets afterwards: 0
// CONCLUSION: After post-processing we got 5143 units of triplet weight, that's 88.87% of total weight (before post-processing this was 88.87%).
// CONCLUSION: After post-processing the symmetric difference is thus 644 + (1 * 1544) = 2188 (before post-processing this was 2188)
// STAT: PERCENTAGE = 88.87
// STAT: NETWORK-TRIPLET SD = 2188
The line beginning // SUMMARY: eNewick output: contains the eNewick representation of the final (i.e. post-processed, where this has not
been switched off) network. (This is the same network as described in the DOT language). The next two lines describe some statistics for the final
network: 644 units of input triplet weight are "missing" from the final network, and the final network has a "surplus" of 1544 triplets. The next
two lines (beginning // SUMMARY: Weight of missing and // SUMMARY: Number of surplus) explain the effect that the post-processing
had. Mild post-processing will never damage any triplets, so the first line will actually always be 0. But some edge contractions performed in the
post-processing might indeed lower the number/weight of "surplus" triplets contained in the network, in which case the second line will be positive.
In this case of this example output file, mild post-processing has had no effect. Note however, that post-processing has clearly done something,
because there are vertices in the final network with outdegree higher than 2. So some edges have been contracted. However, an edge contraction does
not necessarily reduce the number of surplus triplets, as in this case.
The lines // CONCLUSION: are self-explanatory. The final lines, beginning // STAT:, are basically a shorter version of the previous lines. (Such lines are useful when automatically parsing the output in - for example - experiments).
That's pretty much it. If you never use any of the command-line options then your output files will not differ much from the described example. However, LEV1ATHAN is heavily configurable thanks to its command-line options. We now show how they can be used.
--forcemaxsn : this forces the heuristic to -always- use the maximal SN-sets as the blocks of the partition. Only valid when the input is dense. Default is false.
If this option is specified then LEV1ATHAN will never use the heuristic partitioning strategy. To explain: when a triplet set is dense, the maximum SN-sets of this triplet set always form a partition of the leaf-set. This partition is the basis of the polynomial-time algorithms for constructing (where possible) a level-1 network consistent with 100% of the dense triplet set. It seems unlikely that such a partition is a good partition to choose if we want to get consistency with as many input triplets as possible (in the case that 100% consistency is not possible). Nevertheless, if this option is switched on, LEV1ATHAN will always, at every recursion level, use the maximum SN-sets as its partitioning strategy.
One would expect that, if you switch this option on, and feed LEV1ATHAN a dense set of triplets that is 100% consistent with some level-1 network, that LEV1ATHAN will find such a network. This is true. However, in its default mode LEV1ATHAN will do this anyway, even if --forcemaxsn is not specified. That is because, at every recursion level, LEV1ATHAN always checks (in the dense case) first to see if the max SN-sets induce a set of triplets that are 100% consistent with a simple level-1 network, and only if/when that fails will it start heuristically choosing a partition. LEV1ATHAN is thus, in its default mode, a generalisation of the aforementioned polynomial-time level-1 algorithms.
--noperfection : switches off the local perfection test. Default is false.
This is related to the previous point. Even with a non-dense set of triplets it can happen that, at some recursion level, a dense set of triplets emerges and/or that the maximum SN-sets of a non-dense set of triplets coincidentally form a partition of the leaf set. In such cases LEV1ATHAN will check for "local perfection": is the set of triplets induced by the maximum SN-sets 100% consistent with a simple level-1 network? LEV1ATHAN assumes that if this does happen, that it is a good idea to choose this partition. Specifying --noperfection switches such checks off. This only affects the non-dense case: in the dense case "local perfection" is always checked for, and always selected, when it occurs, because of the way JNS moves are defined.
--blocks [num]: this forces the heuristic to always partition into (at most) [num] blocks. Default is 20.
Normally the heuristic partitioning strategy will always add a new block if the scoring function indicates that this would be a good idea. However, it can sometimes be sensible to restrict the maximum number of blocks used by the heuristic partitioning strategy. That is what this option does. Bounding the number of blocks can speed the algorithm up, it can sometimes improve the overall quality of the output network, and it can be of importance for determining the worst-case performance of the algorithm. In particular: if the number of blocks is unbounded then, in really pathological situations, LEV1ATHAN might return networks consistent with less than 5/12 of the input weight (with, in the worst-case, only 1/3 being achieved). In general, however, leaving the blocks unbounded is considered preferable because it allows more freedom to the overall network structure; using --blocks 3 will produce (for example) networks where every gall has exactly three outgoing edges. Note that --blocks 2 will force the output network to be a tree. It is not known how good such trees will be but it can be a useful option if no other tree-building heuristic is available.
(Note that, in reality, the number of blocks is always bounded, because LEV1ATHAN needs to know an upper bound on the number of blocks that will be used. In practice sufficient elasticity in the number of blocks can be achieved by using --blocks to set the upper bound to some very high number).
It can be shown that limiting the number of blocks to 9, safeguards the 5/12 lower bound.
--missing: the heuristic will display all triplets in the input that are not consistent with the output network. Default is false.
Self-explanatory. This concerns the post-processed network. This can be useful for seeing which input triplets did not find their way into the final network.
--surplus: the heuristic will display all triplets in the output network that are not consistent with the input. Default is false.
Similar to the previous option, but with respect to surplus triplets.
--sdradical: perform a radical SD-minimizing post-processing. Default is false. Use in conjection with --sdweight. And with caution!
This option switches on radical post-processing. This is, at the moment, rather unstable. The standard, mild post-processing only contracts edges when this does not lead any of the input triplets that were consistent with the network, to become inconsistent. Mild-processing does not harm the consistency percentage, as it were. However, you might be interested in sacrificing some consistency, to lower the SD score. That is what radical post-processing does. It repeatedly applies the rule "if some edge can be deleted, or contracted, to lower the SD score, then delete (respectively, contract) it" until the SD score can no longer be lowered. As mentioned before, surplus triplets are assumed to have weight 1, unless this has been changed with the --sdweight option below.
Switching on radical post-processing can have curious consequences. For example: if surplus triplets are given (using --sdweight) an excessively high weight, then radical post-processing can sometimes cause the network to 'implode'. So use this option with caution! LEV1ATHAN was mainly designed for maximising consistency, not for minimising SD, so this option is still not fully supported by the developers. It also lengthens the post-processing phase considerably.
--sdweight [num]: when computing the symmetric difference, assume that surplus triplets have weight [num] where [num] is a strictly positive integer. Default is 1.
Self-explanatory (see above also).
--wumax [num]: Wu's algorithm will not be used when there are more than [num] leaves. Default is 10.
Whenever a partition has been chosen with 3 or more blocks, LEV1ATHAN not only tries to find a simple level-1 network consistent with as many of the induced triplets as possible, but also looks at the best tree possible on those induced triplets, and chooses the better of the two. At least, it will do if the induced set of triplets has at most [num] leaves. Setting this value to something small, such as the default 10, is a good idea because the algorithm used is Wu's exponential-time algorithm, and anything considerably higher than 15 can start to really slow things down. In any case the internal implementation of Wu's algorithm has an upper bound of 30 leaves.
--simmax [num]: the exact simple level-1 algorithm will be used for up to and including [num] leaves, the greedy algorithm after that. Default is 12.
The logic here is similar to --wumax. The algorithm for finding the best simple level-1 network is also exponential-time (albeit a lot faster than Wu's algorithm), so it is sensible to say that above a certain threshhold the greedy algorithm for building simple level-1 networks is used, and not the exact one. This option specifies that thresshold. The upper bound is again 30 leaves.
--nopostprocess: do not collapse redundant edges. Default is false.
This completely switches off post-processing: there will be no edge contractions (or deletions) of any kind. For bigger networks this can speed things up considerably. Such networks will always be binary, reflecting the internal functioning of LEV1ATHAN. Unfortunately the computation of edge deletion weights (i.e. the numbers that appear next to the edges) is interwoven with post-processing, so using this option means such weights will not be available in the final network. However, the leaf percentages are still available.
--besttree: builds the optimum tree for the input, and quits. Is exponentially slow! Default is false.
--bestsimple: builds the optimum simple level-1 network for the input, and quits. Is exponentially slow! Default is false.
--bestgreedy: builds the greedy simple level-1 network for the input, and quits. Default is false.
The above three options are utility/test options that allow stand-alone access to some of LEV1ATHAN's subroutines: Wu's algorithm; the exponential-time algorithm to build the simple level-1 network consistent with as many triplets as possible; the greedy algorithm for building a simple level-1 network.
--nonetwork: do not output the network i.e. only output the statistics of it. Default is false.
Self-explanatory.
--dumpnettrips: prints every triplet (irrespective of whether it is in input) that is consistent with the final network to the file 'network.trips'.
Default is false.
--dumpconsistent: outputs to the file 'consistent.trips' the subset of input triplets (including weights) that are consistent with the final network.
Default is false.
Self-explanatory.
--fortyeight: forces the program to produce (via derandomization) the best caterpillar network; this will be consistent with at least 48% of the input triplets, but will be biologically not so meaningful. Switches all other options off!This is another utility option that does not really form part of LEV1ATHAN. It is a rather slow implementation of the "48% algorithm" of Byrka et al (see article). It has been introduced into LEV1ATHAN only for comparison purposes.
--say : 'text', which should be a single word, will be displayed in the information box of the final .dot network produced by the heuristic. There can be multiple --say parameters on the command line.
Self-explanatory.--corrupt [probability]
This option is used for testing. Each triplet that is read in is 'flipped' with the given probability to one of the other two triplet topologies on those three leaves. The topology it flips to is chosen u.a.r. In the output somewhere there will be a line // CORRUPT: which will tell you what percentage of uncorrupted triplets were consistent with the final network. This will be summarised in the line // STAT: PERCENTAGE UNCORRUPTED =. There will also be a field that begins // STAT: NETWORK-NETWORK SD =. This is the symmetric difference between the final network and the network from which the original triplets were drawn. This NETWORK-NETWORK SD statistic (see the two COMMENT lines before it two obtain the two additive components of the SD) thus only makes sense when the original input was exactly equal to the set of triplets in some network.
--sample [probability]
Each input triplet is thrown away with probability (1-[probability]). Again, STAT: NETWORK-NETWORK SD statistics are produced, and - again - we assume the input is equal to all triplets from some network.
We also have several other programs available as part of the LEV1ATHAN package. The most important is NewickToTriplet, a parser written in JavaCC (the Java parser generator: this is something different to the Java compiler!) that converts collections of trees in newick format, to sets of triplets. It should be compiled in the same directory as LEV1ATHAN. We didn't write the actual Newick parser, we adapted the parser found here. On our system NewickToTriplet is built like this:
javacc NewickToTriplet.jj
javac NewickToTriplet.java
Alternatively download the already-compiled JAR file here; in this case it is not necessary to use either javacc or javac.
To use it you need to pipe a text file, where each line is a tree in Newick format, into the standard input channel. For example,
java NewickToTriplet < test1.tre
Or, if you are using the JAR files:
java -jar NewickToTriplet.jar < test1.treIn the generated triplet set a triplet has a weight equal to the number of input trees that it was consistent with, unless the command-line option --noweight is specified. If this is specified then each output triplet will have weight 1.